Figure 2 shows noise levels directly observed with SA.
Figure 2: Noise reduction at room temperature when PD current is 1mA.
Noise levels directly observed with SA are shown. The Poissonian noise level
were obtained with a low efficiency LED (solid line) and a electric bulb
(dotted line).
The noise suppression of 1dB was observed at low frequency range.
The detector photocurrent was 1mA for both Poissonian mode and
sub-Poissonian mode operation.
The load resistance of the photodiode was 1k 
and the reverse-bias
voltage was 9V. When the PD current was reduced to 5 
W, the load
resistance was changed to 10k .
The value of 
was chosen so that LED current became the desired value
for 
V.
The resolution bandwidth of SA was 3kHz and the data is reliable for
frequencies above 20kHz.
Amplifier noise level was obtained when the PD current was zero.
The white light, which was used to determine the Poissonian noise level,
was generated by a low-efficiency LED or a miniature electric bulb which
were driven by a Johnson-noise-limited source. Both light sources gave
the same noise level as shown in Fig. 2.
When the PD current was 1mA, the Poissonian noise level was
13dB above the amplifier noise level at 50kHz.
If we suppose that the amplifier noise consists of only
Johnson-noise of the load resistor, 
, the ratio of the quantum noise
power relative to the amplifier noise power is given by 
,
where V is the voltage across the load resistor.
Note that this is the same relation that appears in Introduction,
where we discuss the condition that the Fano factor of the pump current
is effectively zero.
In this case V=1V and 
mV at room temperature, the ratio of shot noise to Johnson noise is 19 (13dB).
This value is quite consistent with the observed value.
The noise observed with SA, 
, is the sum of the photocurrent
noise power and the amplifier noise power, 
,
Where 
represents the frequency response of the detector and
amplifier system, and 
is the transfer efficiency
which is the product of 
, 
, and 
.
In order to evaluate the normalized noise power (NNP),
we subtract the amplifier noise from the traces in Fig. 2.
Both the Poissonian and the sub-Poissonian noise power decrease
as the frequency increases due to the slow response time of the detection
system. Higher impedance of the load resistor has an advantage of
smaller contribution of amplifier noise , but it has a disadvantage of
slower response time. The NNP is given by the ratio of
sub-Poissonian noise power to Poissonian noise power.
This ratio is independent of detection parameters such as bandwidth
and amplifier gain [18].
So, we will use this NNP in the following discussion.
Figure 3(a) shows the PD current
as a function of the LED current and
Fig. 3(b) shows the mean quantum efficiency
[(PD current)/(LED current), 
] and the differential quantum
efficiency 
as a function of PD current. is
calculated by difference of neighboring data.
Figure 3: (a) PD current as a function of LED current at room temperature (trace i) and at liquid nitrogen temperature (trace ii).
(b) Mean quantum efficiency (trace iii) and differential quantum efficiency (trace iv) at room temperature and these at liquid nitrogen temperature (trace v and vi).
Figure 4 shows the measured NNP for various current levels at room temperature.
Figure 4: Normalized noise power at root temperature for various current
levels.
The noise reduction at low frequencies is 
0.22 when the PD current is
1mA.
By extrapolating the trace, the noise reduction at zero frequency
is given to be 0.23.
For this current level, is 0.18 and is 0.21
as shown by the trace (iii) and (iv) in Fig.3(b).
At higher frequencies, the noise suppression becomes small mainly due
to the slow response time of the LED.
As the LED current decreases, the noise suppression decreases in all
frequency range. This is because the emission efficiency decreases
at low current level as shown in Fig.3.
When the PD current is 50 A, the noise reduction at zero frequency,
, and are 0.15, 0.08, and 0.13, respectively.
When the PD current is 5 A (the light intensity is about 7 W),
these are 0.08, 0.04, and 0.07, respectively.
At room temperature, and decrease rapidly
as the LED current decreases.
Therefore the lowest intensity of sub-Poissonian light is limited to the
order of W.
Note that the amount of observed noise reduction exceeds and
this is inconsistent to the prediction of eq.(1).
There are two possibilities which cause this discrepancy:
the Fano factor of the generated light for sub-Poissonian mode operation
is smaller than 
, or the Fano factor for Poissonian mode
is greater than unity.
Equation (1) is derived from the argument based on a classical stochastic
theory (point process)[19], where it is implicitly assumed that
is equal to .
However, in our experiment is unequal to .
So,
the question we should investigate is what will happen when
differs from .
Since it is not easy to consider the roll of
in a point process picture,
we here examine the meaning of in terms of small-signal transfer.
If 
, the transfer rate of an a.c. signal is larger than a d.c.
component; the ratio of fluctuations to the mean intensity for output is
larger than that for input. Thus the Fano factor of the generated light for
Poissonian mode operation may be larger than unity[20].
Therefore, the discrepancy may be attributed to the uncertainty of the
shot noise power.
A more detailed experimental and theoretical study on this issue
is in progress.
Figure 3 indicates that at liquid nitrogen temperature the emission efficiency changes very little even at very low LED current level. Thus the difficulty of low mean emission-efficiency dose not exist at this temperature. However another problem arises at this temperature. The noise reduction at liquid nitrogen temperature is shown in Fig. 5.
Figure 5: Normalized noise power at liquid nitrogen temperature
for various current levels.
When the PD current is 1mA, the best noise reduction of 0.35 is
realized at 20kHz. As the observation frequency increases,
the noise suppression becomes small more rapidly than in the case of
Fig. 4. And as the current decreases, the noise
suppression for high frequencies disappears.
For example, when the PD current is 5 A, the noise suppression
at 20kHz is 0.25 but it disappears for frequencies above 100kHz.
As explained in Introduction, the noise reduction at the observation
frequency of 
is characterized by the emission efficiency
. Therefore Fig. 5 indicates
that the probability of emission within a short time after the injection
of an electron into the LED becomes smaller when the injection current
is lowered. In other words, the response time of the LED deteriorates
when the injection current decreases. This limited the lowest intensity
of sub-Poissonian light to the order of W in this experiment.
The current-level dependence mentioned above can be understood
by the following models.
At room temperature the emission efficiency decreases as the injection
current decreases.
This is explained by the decrease of injection efficiency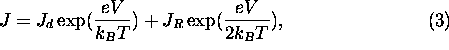 
,
which is defined as the ratio of the diffusion current to the total forward
curret[21].
The total foward current is the sum of the diffusion current and the
generation-recombination current that is due to generation and recombination
through trap states[22]:
where 
and 
are constants which represent the magnitude of
the diffusion current and the recombination current, respectively.
V is the forward bias voltage.
At low values of forward bias, the recombination current dominates and
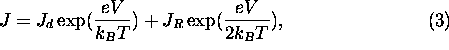is small.
At high forward bias the diffusion current dominates
due to the difference in the exponential multiplier.
At liquid nitrogen temperature the response time of the LED worsened as LED current decreased. This result can be explained by a wavy band model, in which the recombination is from deep localized donor states and deep acceptor states [23]. The recombination time in these states is very long, because the donor and acceptor states are spatially separated due to the wavy band, and so the emission involves long tunneling. At high values of LED current, injected electrons fill the localized states and spatial separation decreases. Thus the frequency response of LED improves.
Note that our results show it is possible to acquire knowledge of carrier' behavior through the study of sub-Poissonian light. Compared to the conventional method that measures the modulation response, this method has the following advantages. First, the measured frequency response reflects only the characteristic of emission process and the effect of detection system is excluded. Second, this method can distinguish whether loss mechanism in light emitting device is stochastic or not: it is shown that current leakage from the lasing junction does not accompany the worsening of the Fano factor in the case of TJS laser[3].