ドップラー冷却について
Ⅰ.
Introduction気体原子ガスにある特定の周波数のレーザーを当てることによって、原子を冷却することができる。レーザーが発明されて以後、1970年代にはレーザーで原子の運動を制御する議論が高まるようになった。
ここではまずその頃の論文である
”Laser cooling of atoms (D.wineland,W.Itano.Phys.Rev.A20,1521(1979)”をもとに、ドップラー冷却というレーザー冷却の最も基本的な原理を紹介する。Ⅱ.ドップラー冷却の原理、および限界
原理について

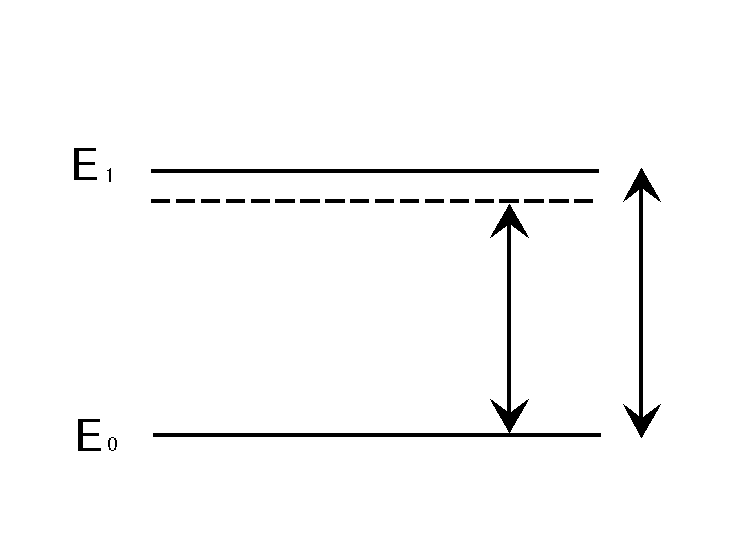
原子がある速度vで運動している場合、簡単の為に話を1次元に限ると次のふたつの場合が考えられる。
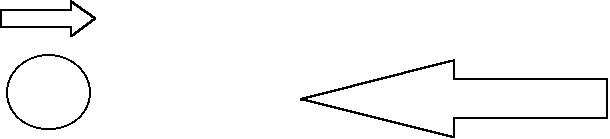
①原子とレーザーの進む向きが逆
②原子とレーザーの進む向きが同じ
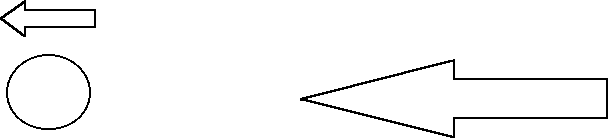
①の場合、原子が感じる光の周波数は大きくなりω0に近くなる。それと反対に②の場合、原子が感じる周波数は小さくなりω0よりさらに遠くなる。つまり①の方が②より光の散乱が起こりやすくなる。
光を散乱する過程(フォトンを吸収して自然放出する過程)において原子の運動量は次のように変化する。
フォトンを吸収する過程
原子は運動量
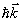
をもらう。
![]()
フォトンを自然放出する過程
原子は有限の運動量変化をする。方向はフォトンを放出する方向の逆。
フォトンを放出する方向はランダムなので平均の運動量変化はゼロとなる。
1つのフォトンが吸収され放出される過程において、速度は平均で
![]()
だけ変化することになる。
このことから原子の進む方向と逆の方向にレーザーをあてれば原子の運動を遮ることができる。ただし、フォトンを放出する過程においての運動量変化は有限である。(方向はランダム) フォトンを吸収する過程に冷却の効果があるのに対し、フォトンを放出する過程においては加熱の効果があるといえる。
これから散乱過程におけるエネルギー変化を見積もることになるが、加熱効果を特徴づける量として以下の量を定義する。
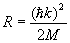
このRをRecoil energyとよぶ。
さて、原子によるフォトンの散乱過程において原子の運動エネルギーがどう変化するか求めたいのだが、その前に吸収光と放出光の周波数を求めることが必要である。
それらは以下の様に記述できる。
![]()
![]()
![]()
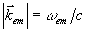
![]()
![]()
![]()
この式は原子とフォトンの運動量とエネルギーの保存から導くことができる。
(1a)式の求め方
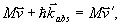
エネルギーの保存式
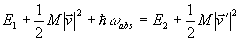
ここで、
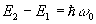
という式を使えば、エネルギーの式は、
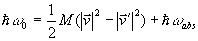
となる。この式に運動量保存の式より得られる、
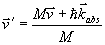
という式を代入すれば、
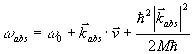
となる。
ここで、
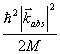
は、Recoil energyに相当するので、(1a)式は導かれたことになる。
また、(1b)式も同じように求めることができる。
さて、この(1a)式と(1b)式を用いて、一回の散乱過程におけるフォトンのエネルギー変化の平均を知ることができる。
フォトンのエネルギー変化は
![]()
である。
平均のエネルギー変化量を求めるには、(1b)式の第二項を無視して(1a)(1b)式を代入すればよい。
(フォトンの再放出過程においてその方向をの平均を取ると0になるとした)
![]()
ここで、一般化する為に波数の添え字をはずしておくと
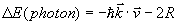
となる。
これにより、原子の運動エネルギー変化は
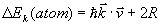
となる。
この式より、
![]()
なら冷却、
![]()
なら加熱が起こることがわかる。
今度はエネルギーの時間変化をもとめる。
まずは原子が1つだけある場合にレーザーを照射した場合を考える。
その場合の散乱断面積は
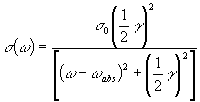
という式で表せる。
ここで、
![]()
は共鳴するときの散乱断面積である。
ここで、
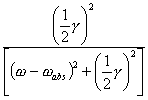
という部分はローレンツ関数と呼ばれ、
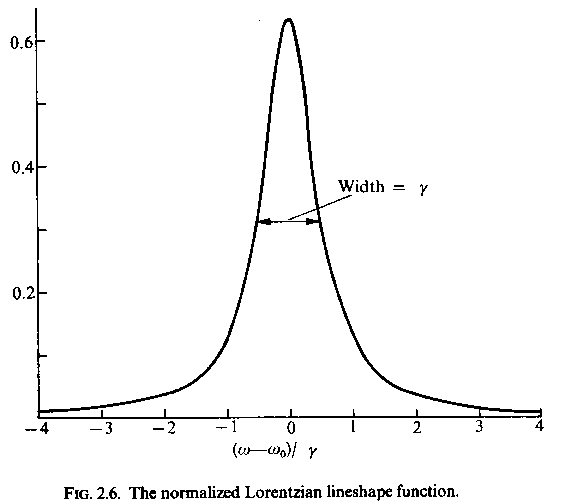
このような形をしている。
さて、これを用いて、運動エネルギーの時間変化は
 (
(
と書ける。
ここで
![]()
はレーザーのエネルギー密度である。
この式は
(単位時間あたりのフォトンの数)×(散乱断面積)×(1回の散乱過程におけるエネルギー変化)
という形になっている。
原子が複数個ある場合は上の式に速度分布関数を掛け、速度空間で積分する。
原子がMaxwell-Boltzmann分布しているとすると、
散乱断面積は
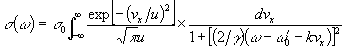
ここで
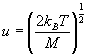
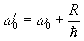
である。
これにより運動エネルギーの時間変化は
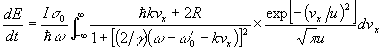
となる。
いままでは原子に1方向からレーザーを照射することを考えてきたが、その場合ある1方向に関しては運動エネルギーを減らす(冷却する)ことができるが、それ以外の方向に関しては逆にRecoil energyによって、運動エネルギーは増えて(加熱して)しまう。
実際に冷却を行うには±x,y,zの6方向からレーザーを照射すればよい。
冷却限界
今までドップラー冷却の原理について紹介してきたが、Recoil energyによる加熱効果によりこの冷却法には限界が存在する。
今まで求めた運動エネルギーの時間変化より、その限界を見積もることができる。
まずは、以下のことを仮定する。
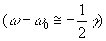
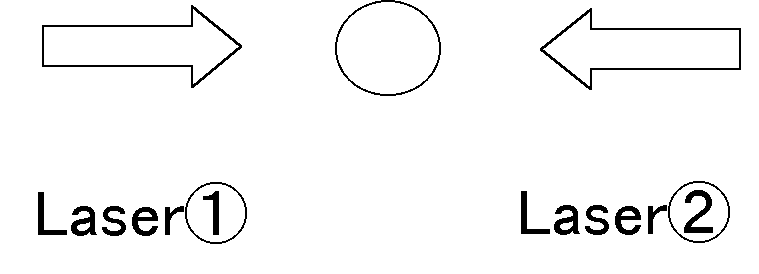
この場合のエネルギーの時間微分は
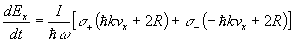
となる。ただし、簡単の為にx成分のみを考えることにした。
ここで、
![]()
はLaser①が原子に当たった場合の散乱断面積であり、
![]()
はLaser②が原子に当たった場合の散乱断面積である。
この散乱断面積の式は以前に求めた(3)式により
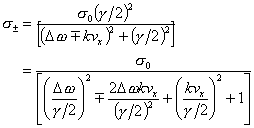
と書ける。
ただし、
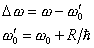
である。
ここで
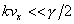
なので、
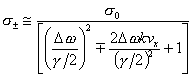
となる。
これを
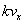
でテーラー展開すると、
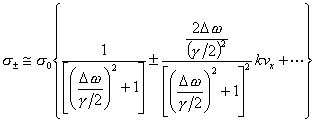
となる。
これを用いれば、エネルギーの時間変化の式は
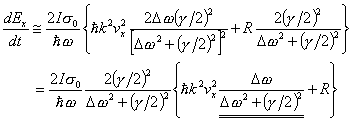
となる。この下線部に注目する。
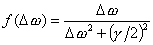
として、Δωで微分すると
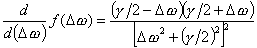
となる。
これによりf(Δω)は
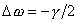
のときに最低になる。
つまり、
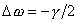
のときに、最も冷却することができる。(最適な離調である、といえる)
この周波数のときにおけるエネルギー平均値の時間微分は
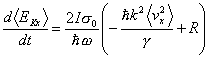
となる。
この運動エネルギーの平均値の最小値は
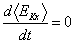
のときに得ることができる。
すると、
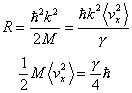
という式から
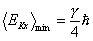
となる。冷却限界は自然幅できまることがわかる。
もし、原子がMaxwell-Boltzmann分布に従うとすれば、
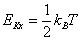
となる。
自然幅を
![]()
とした場合、(Naの場合に相当する)
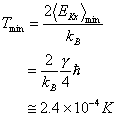
となる。
Ⅲ.初めて行われた3次元的ドップラー冷却の実験
はじめて3次元的ドップラー冷却の実験が行われたのは1985年のことである。(S. Chu, L. Hollberg, J. E. Bjorkholm, A. Cable, and A, Ashkin, Phys. Rev. Lett. 55 ,48(1985).)
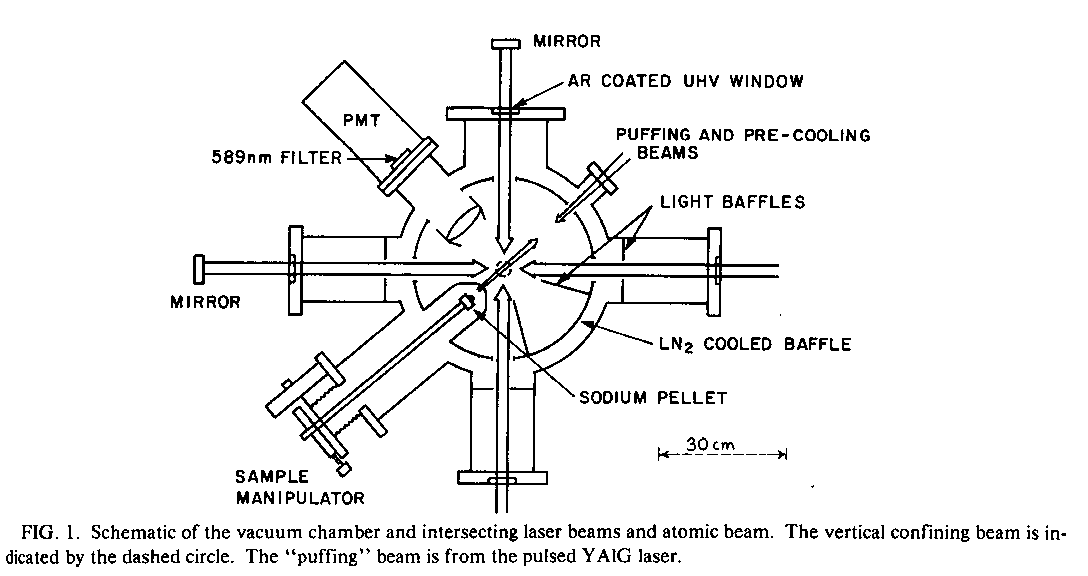
この実験ではNaの原子を上の結果とあう240μKまで冷却することに成功した。
Ⅳ.まとめ
以上、ドップラー冷却の原理を紹介した。
最適な周波数は
![]()
のときで
冷却限界は
![]()
である。