遠心力について

遠心力と向心力

高校で必ず一度はこんがらがる「遠心力」と「向心力」の違い、これは簡単なように話している人を大勢見掛けるが、自分にとってはいまだに難しい問題である。だから、よくわからなくていいとも思う。もちろんわかっていたほうが良いのだが…。中途半端にわかろうとせず、何がわからないのかをはっきりさせること、わからない所をあら捜しすること、それについて自分で考えてみること、これが一番の近道なような気がする。自分の視点で遠心力を考察する。

等速円運動に関して

まず、力がかかっていないときこのときは等速直線運動をします。これは慣性の法則より、「動いている物は動き続けるから、力がかかっていないときは等速直線運動をする」といってよいだろうし、運動方程式からも導いてもよいと思います。
（今調べてみたら、慣性の法則は「運動の第一法則」というものであった。これとF=maと、いう「運動の第二法則」を組み合わせたものが運動方程式らしい。だから、運動方程式と慣性の法則は同じ立場ではなく、運動方程式は慣性の法則を含んでいるのだ（たぶん））
逆に力がかかっていないときは等速直線運動をするといえます。
（大学生向け注…すべての力の和が０ベクトルのときで、さらにモーメントベクトルの和が０のときに剛体が等速直線運動をする。モーメントが０でないと、力の和が０でも剛体が回転してしまう）。
円運動はまっすぐではなくまがった軌道をしてますよね？だから円運動をするためには、なにかしらの力が働いていないと等速円運動できません。

等速円運動するためには力が必要なことがわかりました。ではどんな力が必要なのでしょうか？まずいえることは、等速円運動なので、つねに等しい速度で回転しているわけです。力がかかっても、速度が速くならないためには、進行方向に垂直な方向に力がかかっている必要があります。円運動に関して言えば、つねに進行方向に垂直な向きとは、その回転の中心方向です。また力の大きさは、対称性により常に等しい力がかかっていると言えます。つまり、等速円運動をするためには、つねに中心方向のみの等しい力が働いていることがわかります。もしそれ以外の力が働いていたら、必ず等速ではなくなるので、そう結論することができます。

いま僕たちは、ぐるぐる回っている物体を眺め、それからわかることを導きました。ぐるぐる回っている物体を見ているのです。これが重要だと思います。それからわかったことは、中心方向に等しい力がかかっているということだけです。この
円運動を眺めているとき明らかに分かるように、その物体にかかっている力というものは円の中心に向かった力である。つまりこの力を「向心力」と呼ぶのである

遠心力とは…

では遠心力となんでしょうか？自分たちが車に乗っていて急カーブしたとき、またはジェットコースターにん乗ったとき、感じる力は間違いなく向心力とは逆向きの力つまり遠心力を受けているように感じます。

車が右に曲がるときを考えてみましょう。
車が右に曲がるときは、当然右向きの加速度を車に働かせないと曲がれません。まぁただ単にハンドルを右に切ればいいんですが…。右に切って、向心力を車に働かせます。車は右に進もうとしますが、中に乗っている人は真っ直ぐ進もうとします。だから、中に乗っている人は車から右向きに押されるわけです。これを体が円の外の方向に押されているように感じる、つまり遠心力を受けていると感じているわけです。
もう一度言いますと、車が右に曲がるとき、車が右に中の人を押しているのです(だから中の人も右に曲がることができる)。しかし、車が押してくるのではなく、自分に力が働いたと勘違いしたものが遠心力なんです。ここで図を使った説明を

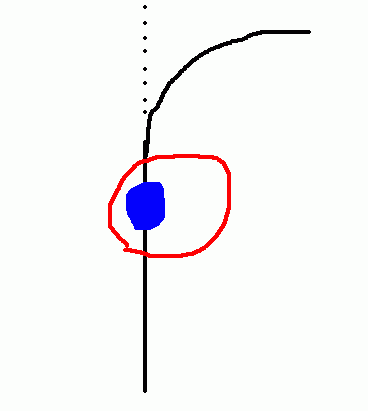
へたくそな図ですが…赤い丸が車です。青い丸が人です。黒い線に沿って車が走ろうとしてます。初めは真っ直ぐ進んでいるので、人も車も直線運動です。車が右に曲がりはじめます。が、ひとは感性の法則より、まっすぐ点線上を進もうとします。が、車は曲がるので、必ず車の左側から右向きに人が押されます。しかし人はこの現象を、左に力がかかっているように感じてしまうので、これを遠心力と呼ぶのでした。

これからわかるように、遠心力とは見せ掛けの力で、実際に働いている力は向心力なのでした。なのに普通は「遠心力がすごい」とか、よく使われるのは遠心力の方ですが、その気持ちはすごくわかります。友達も｢電車がゆれたら、向心力が・・・とか考えちゃうからやだね｣とか言ってましたが、これを読んだあなたもそうなってしまう一人なのです!!

すべて私の考えですので間違っていることが十分考えられます。
いろいろなご意見待っております

メール HOME