検出器の雑音レベルと量子雑音レベルの絶対値について

1. 反転増幅器の雑音

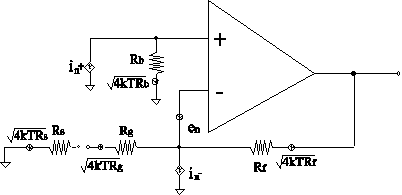
図１のようなオペアンプで構成された反転増幅器を考える。この回路の雑音源は次の３種類が考えられる。最初の二つは増幅器に固有のもので、intrinsic input voltage noise (en)と、intrinsic input current noise(in=in+=in-)である。三つめは、外部抵抗に起因する熱雑音である(et=Sqrt[4ktR])。

増幅器の等価入力雑音密度はこれらの和として、次式のように表せる。

(1)

ここで簡単のために、Rb=0、Rs=0、Rg<<Rsとすると、この場合の等価入力雑音密度は次式で表される。

(2)

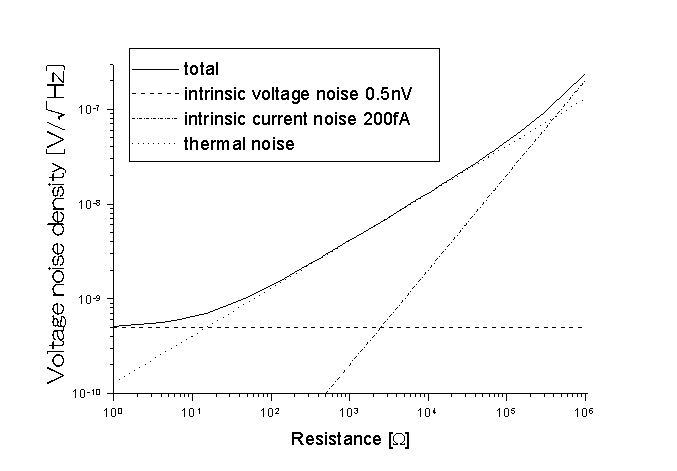
エヌエフ回路製FET増幅器SA-220F5の場合、入力換算雑音電圧密度は、0.5nV/typ、入力換算雑音電流密度は、200fA/typと与えられているので、これを上式に代入し、等価入力雑音密度を外部抵抗の関数としてプロットした結果を図２に示す。この図から、負荷抵抗の小さい領域では、増幅器の雑音電圧が、大きな領域では雑音電流の寄与が支配的であり、中間領域の負荷抵抗が概ね100〜10kΩの場合には、抵抗の熱雑音が支配的であることが分かる。我々の実験の場合、抵抗値はこの領域にあるので、増幅器の雑音として、熱雑音の寄与を主に考えればよいことが分かる。

この節では、増幅器の入力抵抗を変えたときに、スペクトラムアナライザで実際に観測される雑音レベルと、熱雑音から見積もった雑音レベルとの比較を行う。上述のように抵抗Rの両端に現れる熱雑音電圧密度は次式で表せる。

(3)

Tは抵抗の温度、kはボルツマン定数である。周波数fにおける増幅器の電圧利得をg(f)とすると、増幅された雑音電圧密度は、

(4)

となる。増幅器の出力インピーダンスとスペクトラムアナライザの入力インピーダンスは等しく、共にRsであるとすると、増幅された熱雑音のパワー密度は、

(5)

である。スペクトラムアナライザの入力フィルターをR(f)とする。R(f)の関数形は、スペクトラムアナライザの仕様に依存するが、ガウス関数の場合は、

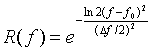(6)

ローレンツ関数の場合は、

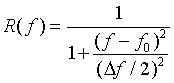(7)

と表される。f0は中心周波数、Δfは分解能帯域幅(resolution band-width:RBW)である。結局観測される雑音レベルは、

(8)

となる。増幅器の利得が周波数に依らず一定と仮定し、g(f)=g0とおくと、

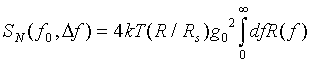(9)

となる。積分の部分は、ガウス関数の場合は、

(10)

ローレンツ関数の場合は、

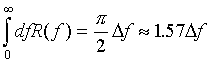(11)

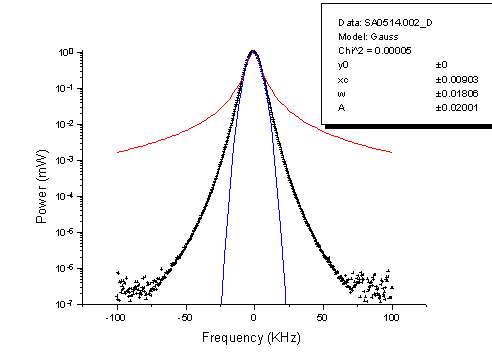
である。アンリツのスペクトラムアナライザMS2601Bで分解能帯域幅を10kHzに設定したときのフィルタの形状の実測した結果を図３に示す。測定は、HPの信号発生器HP8648Bを使って、周波数1MHzの正弦波を発生させ、そのパワーを測定した。元の正弦波のスペクトル幅が十分狭いとき、測定されるデータは、フィルターの関数形を反転したものになる。この結果から、フィルタの関数形は、ガウスとローレンツの間にあり、ガウシアンで良く近似できることが分かる。この場合、観測される雑音レベルは、

(12)

である。この式を使って、測定された雑音レベルから、入力換算雑音密度を計算することもできる。

SA-220F5の入力抵抗を変化させたときの、検出器の雑音レベルの測定結果を図４に示す。(8)式あるいは(12)式から期待されるように、測定される雑音レベルは、抵抗値が大きくなるに従って大きくなる。抵抗値が1KΩの場合には、高周波側で雑音レベルが減少している。この理由は、負荷抵抗に並列にフォトダイオードが接続されている状態で測定を行ったので、周波数が高くなるに従ってインピーダンスが小さくなるためだと思われる。図４のグラフからゼロ周波数における雑音レベルを読みとった結果を表１と図５に示す。SA-200F5の電圧利得のカタログ値は、50Ω負荷に対して200倍である。(12)式を用いて入力での電圧密度に換算した結果を同じく表１に示す。比較のために、熱雑音の理論値も示した。負荷抵抗が0Ωの時は、intrinsic input voltage noiseのみ寄与するはずであるが、実験から見積もった電圧密度は、0.332nV/でカタログ値の0.5nV/より３割強小さい。負荷抵抗が有限の値の場合の入力換算電圧密度の値は、熱雑音理論値のSqrt[4kTR]より小さい。入力換算電圧密度から、0Ωの時の値を差し引きし、熱雑音相当分の電圧密度と、理論値を比較すると、いずれも2〜3割程度小さい。

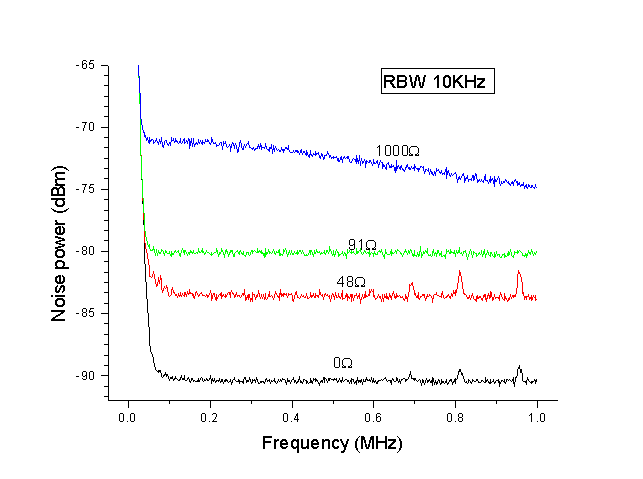
図４　検出器の雑音レベルの抵抗値依存性

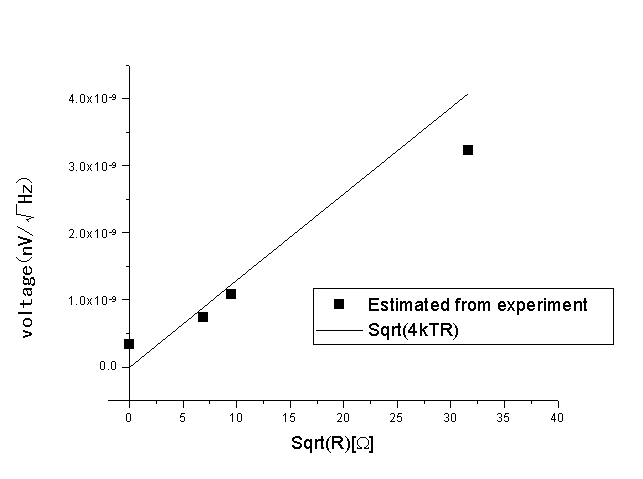
図５　入力換算電圧密度

測定された検出器の雑音レベルから見積もった入力換算電圧密度は、熱雑音理論値よりも小さいという結果が得られた。見積もり値は、スペクトラムアナライザのフィルターのバンド幅と、増幅器の利得に依存している。バンド幅に関しては、上述のように実測しており、またガウス関数を仮定しているので、むしろ小さめの見積もりになっている。利得に関して実測をまだ行っていないので、今後検討の必要がある。

表１　入力換算電圧密度の見積もり

3. ショット雑音レベル

電流iに伴うショット雑音の大きさは、帯域幅δfに含まれる電流の揺らぎとして次式で表される。

(13)

eは素電荷である。増幅器が電圧増幅器であることを考慮して、抵抗値Rを掛けることで電圧の揺らぎに直し、

(14)

電圧利得g(f)を掛けると、

　 (15)

となるので、スペクトラムアナライザ入力端でのパワーは、(5)式のように、入力インピーダンスRsで割って、

　 (16)

である。結局、測定される雑音レベルは、スペクトラムアナライザの入力フィルタをR(f)を使って、次式で与えられる。

(17)

(9)式と同様に、利得が周波数に依存しないとすると、

　 (18)

となる。さらに、フィルターの関数形を(6)式で与えられるガウシアンだと仮定すると、(12)式と同様に、

(19)

4. 熱雑音とショット雑音の比

熱雑音とショット雑音の絶対レベルの見積もりは、(12)、(19)式のように増幅器の利得とスペクトラムアナライザのフィルターの帯域幅に依存しており、さらにフィルターの関数形にも依存している。しかし、二つの雑音の相対的な強度比は、(8)式と(17)式の比で与えられ、これらに依存しない。

(20)

ここで、Vは負荷抵抗での電圧降下を表しており(V=iR)、電圧降下の量が与えられれば、測定状況に依らず、二つの雑音の強度比が決まる。

1章で述べたような増幅器の雑音の原因を熱雑音のみと見なして良い場合には、増幅器の雑音レベルとショット雑音レベルの強度比は、測定状況に依らず、負荷抵抗での電圧降下の量だけで決まることになる。

ポアソンモードの雑音が、ショット雑音と熱雑音の雑音の和であると考えれれると、対数で表したノイズパワーの差は、

(dBm) (21)

と予測される。今、V=165mVで、室温では2kT/e=52mVであるから、ノイズパワーの差は6.2dBとなる。図６のデータのポアソンモードと増幅器の雑音レベルの差をプロットした結果を、図７に示す。1MHz以下の過剰な雑音を除けば、6dB弱の差であり、一致していると言える。多少小さな値であるのは、増幅器の雑音が熱雑音のみより大きいためであると思われる。

図６　ショット雑音の測定例

図７　Poisson modeとamplifier noiseの比